Pythagorean Means

Posted on In , Views: Word count in article: 255 Reading time ≈ 1 mins.

2D

definition

  • quadratic mean/root mean square := $\sqrt{\frac{1}{2}(a^2+b^2)}$
  • arithmetic mean := $\frac{a+b}{2}$
  • geometric mean := $\sqrt{ab}$
  • harmonic mean := $(\frac{1}{2}(\frac{1}{a}+\frac{1}{b}))^{-1}$

TH

$$
max(a,b) \ge QM/RMS \ge AM \ge GM \ge HM \ge min(a,b)
$$
We can prove it as below:

geometry prove 1

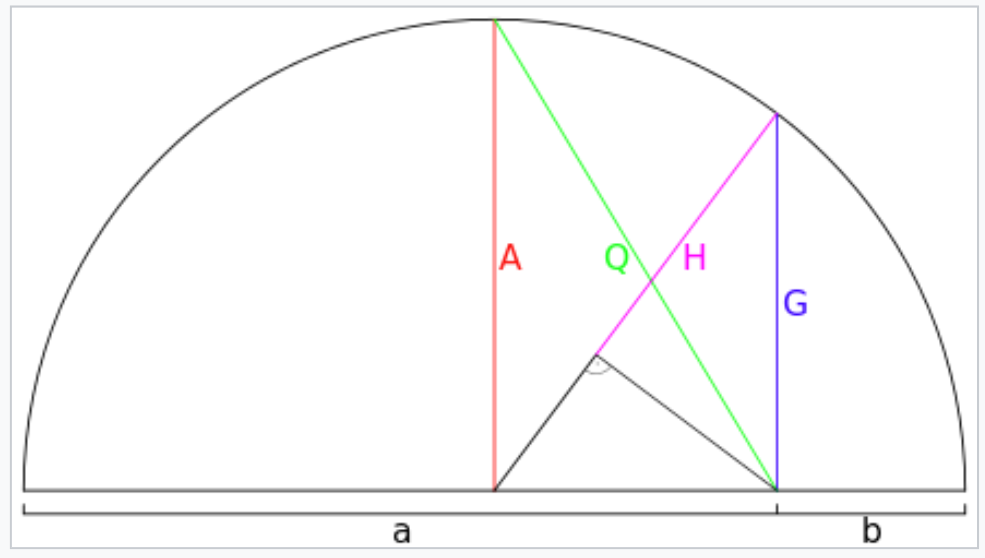
  • $max(a,b) \ge QM/RMS$: use angle
  • $QM/RMS \ge AM$: obviously
  • $AM \ge GM$: obviously
  • $GM \ge HM$: obviously
  • $HM \ge min(a,b)$: think about their dual length, i.e.: $AM-HM$ and $AM-min(a,b)$

geometry prove 2

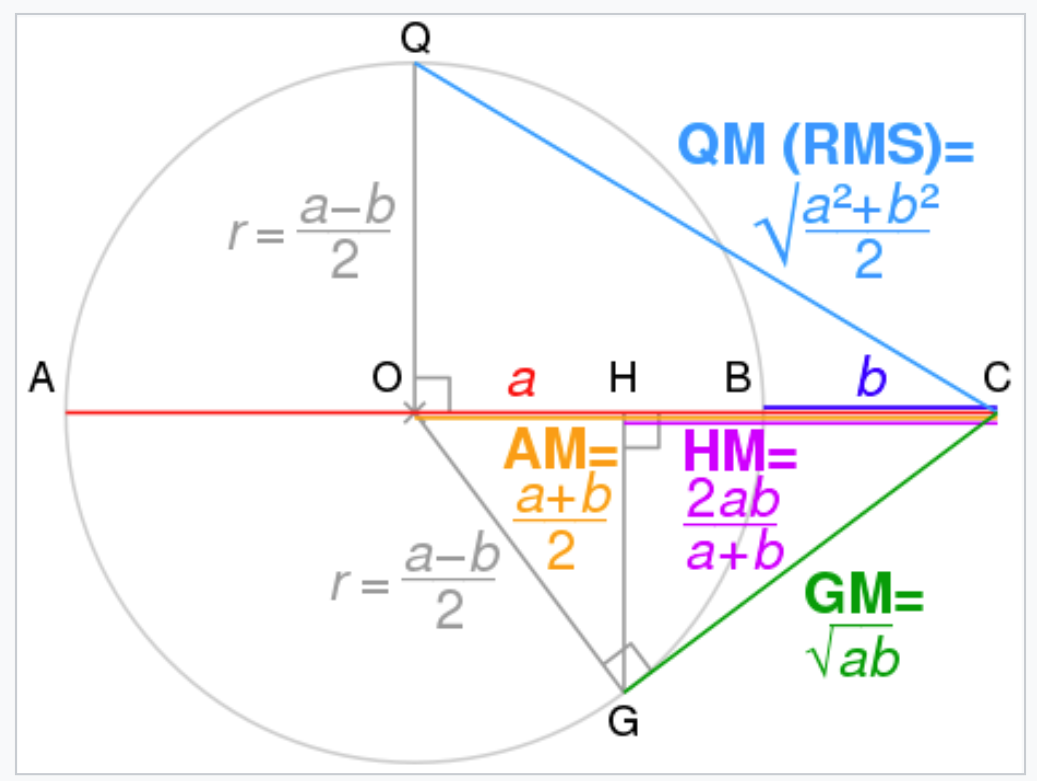
  • similar to geometry prove 1

more than 2D

definition

  • quadratic mean/root mean square := $\sqrt{\frac{1}{n}(x_1^2+x_2^2+…+x_n^2)} = \sqrt{<X^2>} = <X^2>^{\frac{1}{2}}$
  • arithmetic mean := $\frac{x_1+x_2+…+x_n}{n} = = <X^1>^1$
  • geometric mean := $\sqrt{x_1x_2…x_n}$
  • harmonic mean := $(\frac{1}{n}(\frac{1}{x_1}+\frac{1}{x_2}+…+\frac{1}{x_n}))^{-1} = <\frac{1}{X}>^{-1} = <X^{-1}>^{-1}$

TH

We still have
$$
max(x_1,x_2,…,x_n) \ge QM/RMS \ge AM \ge GM \ge HM \ge min(x_1,x_2,…,x_n)
$$
The prove is omitted

generalization

$Hölder \ mean := <X^p>^{\frac{1}{p}}$

  • We can prove that $\displaystyle \lim_{p \to 0} Hölder \ mean = GM$
  • We can prove that $p \nearrow \Rightarrow Hölder \ mean \nearrow $

By the way, We can call Hölder mean “1/p-mean-p” in analogy of “root-mean-square”